You are in Home page » Documentation » Quantum anomaly

|
You are in Home page » Documentation » Quantum anomaly |

|
|
Next: Bibliography Up: Anomalie quantistiche Previous: La simmetria chiriale e L' anomalia ABJ con il metodo perturbativoVediamo ora di attaccare lo stesso problema utilizzando il metodo perturbativo dei diagrammi di Feynman alla maniera di Adler [1]. Riscriviamo la I.15 nella forma
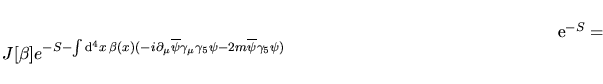 da graficamente le usuali regole di Feynman per la QED mentre il
termine aggiuntivo nella sua parte indipendente da da graficamente le usuali regole di Feynman per la QED mentre il
termine aggiuntivo nella sua parte indipendente da ![[*]](footnote.png) da, se accoppiato a una sorgente esterna
da, se accoppiato a una sorgente esterna
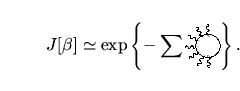 i grafici a due linee fermioniche contenenti un vertice
i grafici a due linee fermioniche contenenti un vertice
e con 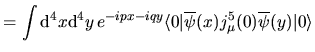 i grafi a due linee fermioniche esterne conteneni
un vertice i grafi a due linee fermioniche esterne conteneni
un vertice
Allora se si considera l' usuale equazione del moto si ottiene,come visto sopra per la divergenza il valore errato I.8. Da questa espressione si possono ricavare le così dette Ward identities utilizzando la [5] _0| j_^5(x)_i_i(x_i)|0&= &0|_j_^5(x)_i_i(x_i)|0- & &-i_i(x-x_i)0|_i(x_i)_ji_j(x_j)|0 Esplicitando tale formula in questo caso e ricordando la I.8 si ha che ![$\aligned
\lim_{z\to0}
\partial_\mu^z{\langle{0}\vert} \overline{\psi}(x)j_\mu...
...gamma_5\overline{\psi}(y))\overline{\psi}(x){\vert{0}\rangle})\bigr]\endaligned$](img186.png) dove l' ultima si ha ricordando la I.5. Passando ora allo
spazio di Fourier e dimenticando le costanti di normalizzazione
che si semplificano ad ambo i termini si ha che
dove l' ultima si ha ricordando la I.5. Passando ora allo
spazio di Fourier e dimenticando le costanti di normalizzazione
che si semplificano ad ambo i termini si ha che
![$\aligned
&\lim\limits_{z\to 0}\partial_\mu^z \int {\rm d}^4p\,{\rm d}^4q\,
e^...
...t {\rm d}^4p\,{\rm d}^4q\, e^{ipx+iqz}S_F(q+p)\gamma_5\right]}$}}}
\endaligned$](img187.png)
![$\aligned
&-\lim\limits_{z\to 0}i(p+q)\int {\rm d}^4p\,{\rm d}^4q\,
e^{ipx+iqy...
...int {\rm d}^4p\,{\rm d}^4q\, e^{ipx+iqz}S_F(q+p)\gamma_5\right]}$}}}\endaligned$](img188.png) Ora, nel membro a sinistra e nel primo membro a destra si può eseguire tranquillamente
il limite senza problemi, negli ultimi due membri di sinistra si può
formalmente sostituire al limite per
Ora, nel membro a sinistra e nel primo membro a destra si può eseguire tranquillamente
il limite senza problemi, negli ultimi due membri di sinistra si può
formalmente sostituire al limite per 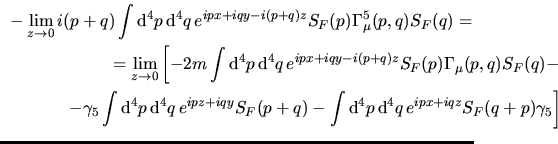 rispettivamente un limite per rispettivamente un limite per
 e quindi
e quindi
Ciò che intendiamo mostrare ora è che queste non valgono in un calcolo perturbativo e che il termine aggiuntivo è proprio il termine anomalo della I.49. Nell' idea di sviluppare le Ward identities in un ambito perturbativo scriviamo
dove
Ora, allo scopo di derivare le I.61 in modo diagrammatico si può operare una classificazione dei diagrammi che contribuiscono a formare  in due classi: in due classi:
![[*]](footnote.png) .
Ora il generico dermine dei diagrammi del secondo tipo con .
Ora il generico dermine dei diagrammi del secondo tipo con ha solo due fotoni uscenti e dunque esso risulta linearmente divergente e quindi l' operazione di ridefinizione dell' integrale sul loop non è più lecita. Ciò che accade dunque, per questo diagramma, è che detto con 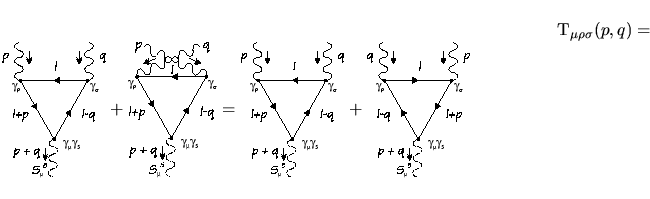 il grafo a triangolo con le linee esterne segate ossia tale che il grafo a triangolo con le linee esterne segate ossia tale che
 e quando si applica una traslazione nella misura
d' integrazione si ha che e quando si applica una traslazione nella misura
d' integrazione si ha che
![$\aligned
T_{\mu\rho\sigma}(p,q)
&=(-1)\mathop{\famzero Tr\,}\nolimits \displa...
...\hskip-0.05em{\ell}\,$}+\makebox{$\not\hskip-0.18em{p}\,$}}\right]
\endaligned$](img212.png) e dunque
e dunque
Come già detto questi integrali risultano linearmente divergenti in quattro dimensioni. L' idea immediata sarebbe di valutare la traccia e poi l' integrale ma dato che si lavora nell' ambito della regolarizzazione dimensionale ciò non funziona perchè la 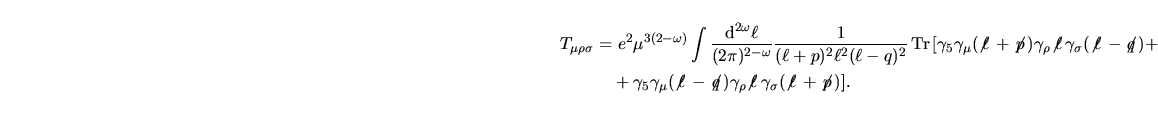 e ciò che rimarrà
sara la traccia di e ciò che rimarrà
sara la traccia di
![$\aligned
T_{\mu\rho\sigma}(p,q)
&=2e^2\mu^{3(2-\omega)}
\displaystyle\int \d...
...ell(py-qx)
+p^2y+q^2x]^3}
\mathop{\famzero Tr\,}\nolimits [\cdots]\endaligned$](img218.png) e detto con
e detto con
![$\aligned
T_{\mu\rho\sigma}
&=2e^2\mu^{3(2-\omega)}
\displaystyle\int _0^1\!{...
...5em{\ell}\,$}\gamma_\sigma\makebox{$\not\hskip-0.18em{p}\,$})\bigr].\endaligned$](img220.png) Come si vede
Come si vede
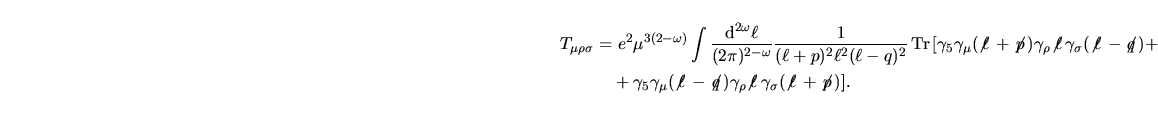 possiede termini lineari quadratici
e cubici in possiede termini lineari quadratici
e cubici in 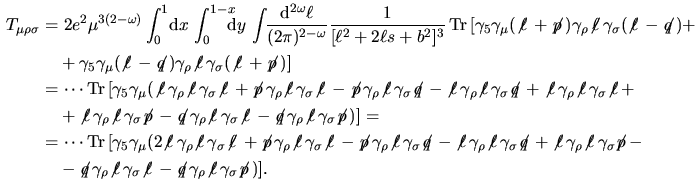 . Al fine di semplificare le cose eliminando il termine
cubico ricordando che . Al fine di semplificare le cose eliminando il termine
cubico ricordando che
![$\aligned T_{\mu\rho\sigma}(p,q)
&=\cdots\mathop{\famzero Tr\,}\nolimits \bigl[...
...p-0.05em{\ell}\,$}+\text{ termini lineari e quadr. in }\ell)\bigr]
\endaligned$](img223.png) d' altra parte
d' altra parte
![$\aligned
T_{\mu\rho\sigma}(p,q)
&=\cdots\mathop{\famzero Tr\,}\nolimits \bigl...
...\\
&\quad-
\ell_\beta (p_\alpha q_\delta-q_\alpha p_\delta)\bigr]\endaligned$](img225.png) per cui i termini da valutare sono
per cui i termini da valutare sono
T^(2)_&=& 2e^2^3(2-) _0^1dx_0^1-xdy d^2(2)^2- __(p_-q_)+ __(p_-q_) [^2+2s +b^2]^3· & &·Tr[_5___ __] T^(3)_&=& 2e^2^3(2-) _0^1dx_0^1-xdy d^2(2)^2- -_(p_q_-q_p_) [^2+2s +b^2]^3· & &·Tr[_5___ __] e d' altra parte, ricordando che ![[*]](footnote.png) d^2(2)^2-
_[^2+2s
+b^2]^3&=&
-(3-)(4)^(3)s_(b^2-s^2)^
3-
d^2(2)^2-
_[^2+2s
+b^2]^3&=&
-(3-)(4)^(3)s_(b^2-s^2)^
3-
d^2(2)^2- __[^2+2s +b^2]^3&=& 1(4)^(3){12_ (2-)(b^2-s^2)^2-+. & &.+(3-) s_s_(b^2-s^2)^3-} mentre, derivando ulteriormente rispetto a 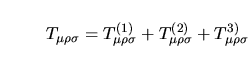 la
d^2(2)^2-
__[^2+2s
+b^2]^A&=&
1(4)^(A){12_
(A-1-)(b^2-s^2)^A-1-+. la
d^2(2)^2-
__[^2+2s
+b^2]^A&=&
1(4)^(A){12_
(A-1-)(b^2-s^2)^A-1-+.
& &.+(A-) s_s_(b^2-s^2)^A-} si ha che 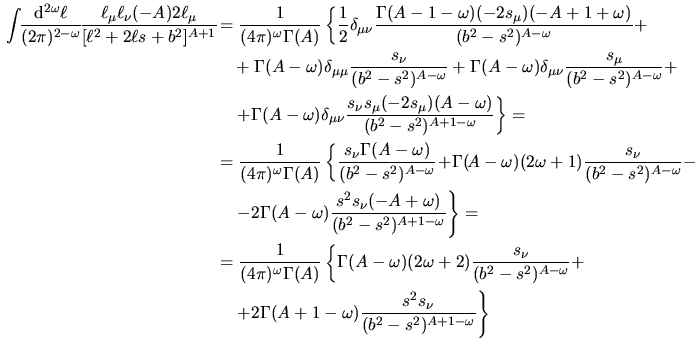
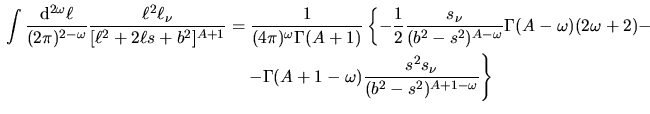 si ha che
d^2(2)^2-
^2_[^2+2s
+b^2]^A&=&-
1(4)^(A){
s_(b^2-s^2)^A-1-(A-)(+1)+. si ha che
d^2(2)^2-
^2_[^2+2s
+b^2]^A&=&-
1(4)^(A){
s_(b^2-s^2)^A-1-(A-)(+1)+.
&&.+ (A-)s^2 s_(b^2-s^2)^A-}. Partiamo allora con il calcolare
![$\aligned
T^{(1)}_{\mu\rho\sigma}(p,q)&=
4e^2\mu^{3(2-\omega)}\displaystyle\i...
...}\nolimits [\gamma_5\gamma_\mu\gamma_\rho\gamma_\sigma\gamma_\alpha]\endaligned$](img234.png) Si tratta ora di regolarizzare questo grafico usando l' approccio
dimensionale
Si tratta ora di regolarizzare questo grafico usando l' approccio
dimensionale
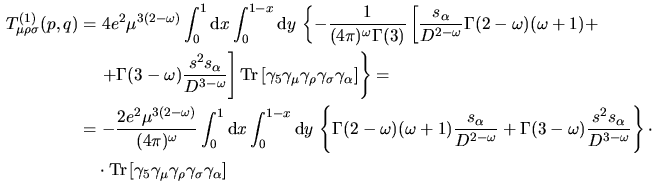
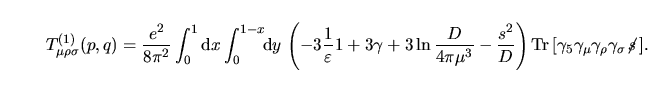 utilizzando la I.74 utilizzando la I.74
![$\aligned T^{(2)}_{\mu\rho\sigma}(p,q)
&=e^2\mu^{3(2-\omega)}\displaystyle\int ...
...a_\alpha\gamma_\rho\gamma_\beta
\gamma_\sigma\gamma_\delta]\biggr\}\endaligned$](img240.png) ma
ma
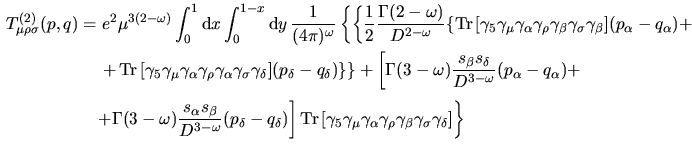 per cui
per cui
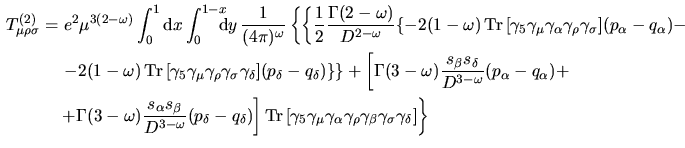 perchè in tali termini ci sarebbe la traccia di
una perchè in tali termini ci sarebbe la traccia di
una & &-2____+ 2____- 2____- _____ e inserito questo risultato nel termine della seconda traccia proporzionale a 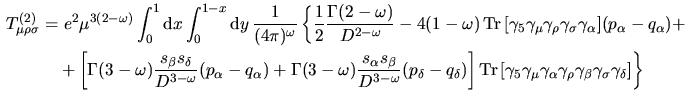 produce, a parte il segno,
come ultimo termine proprio
quello proporzionale a produce, a parte il segno,
come ultimo termine proprio
quello proporzionale a
![$\aligned
T_{\mu\rho\sigma}^{(2)}
&=e^2\mu^{3(2-\omega)}\displaystyle\int _0^1...
...ma_\rho\makebox{$\not\hskip-0.18em{s}\,$}]s_\sigma
\right\}\biggr\}\endaligned$](img248.png) d' altra parte anche per questi termini vale il fatto che si può anticommutare
senza il termine con la delta per cui
d' altra parte anche per questi termini vale il fatto che si può anticommutare
senza il termine con la delta per cui
![$\aligned
T_{\mu\rho\sigma}^{(2)}
&=e^2\mu^{3(2-\omega)}\displaystyle\int _0^1...
...ma_\rho\makebox{$\not\hskip-0.18em{s}\,$}]s_\sigma
\right\}\biggr\}\endaligned$](img248.png) per cui il secondo e il quarto si elidono a vicenda.
Passiamo a regolarizzare i termini rimasti
per cui il secondo e il quarto si elidono a vicenda.
Passiamo a regolarizzare i termini rimasti
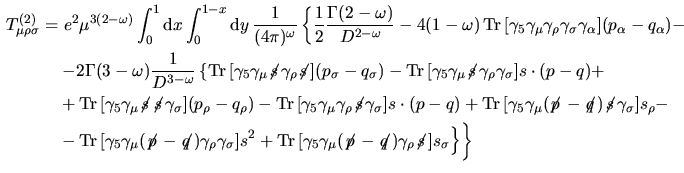 e dunque ordini finiti si ha che
e dunque ordini finiti si ha che
Passiamo infine a calcolare 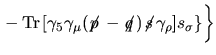 utilizzando la I.73 e con lo stesso metodo
utilizzato sopra si giunge a utilizzando la I.73 e con lo stesso metodo
utilizzato sopra si giunge a
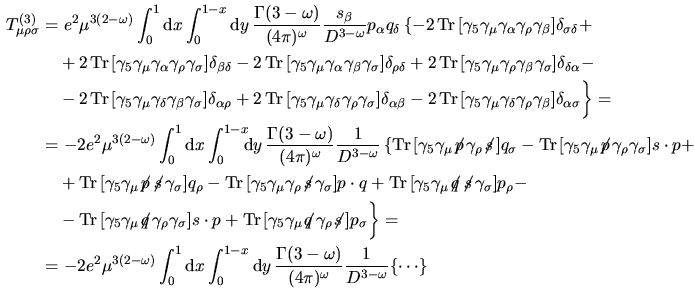 e quindi ordini finiti si ha che
e quindi ordini finiti si ha che
Vediamo allora di risommare i vari termini ordine per ordine. Ordini 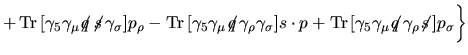 si ha che si ha che
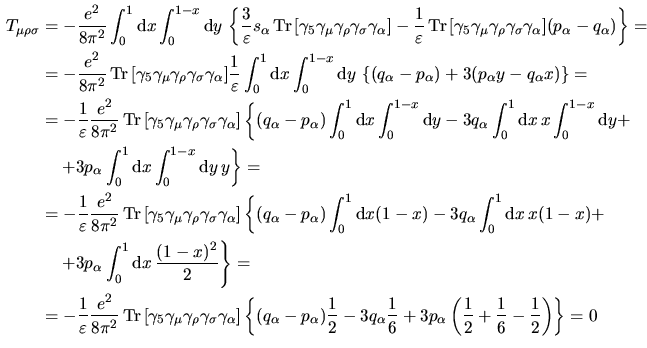 siano singolarmente divergenti per
siano singolarmente divergenti per 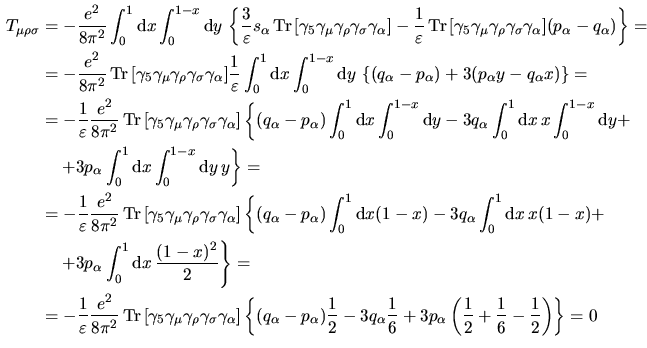 Possiamo a questo punto eliminare ulteriormente i termini contenenti il logaritmo
con la seguente considerazione: tali diagrammi contengono, così come
sono una divergenza infrarossa ma, come la I.62 non
contiene divergenze ultraviolette si può anche dimostrare che esso non contiene
divergenze infrarosse e dunque tali termini devono necessariamente annullarsi.
Allora ciò che resta è il solo termine proporzionale a
Possiamo a questo punto eliminare ulteriormente i termini contenenti il logaritmo
con la seguente considerazione: tali diagrammi contengono, così come
sono una divergenza infrarossa ma, come la I.62 non
contiene divergenze ultraviolette si può anche dimostrare che esso non contiene
divergenze infrarosse e dunque tali termini devono necessariamente annullarsi.
Allora ciò che resta è il solo termine proporzionale a  Allora anche il termine proporzionale a
Allora anche il termine proporzionale a 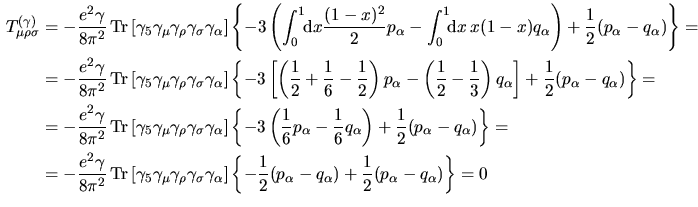 contenente il solo contenente il solo ![[*]](footnote.png) .
Chiamiamo con .
Chiamiamo con
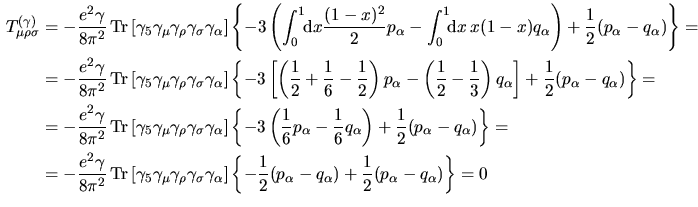 e
in e
in
![[*]](footnote.png) che il primo termine si può riscrivere di modo che
che il primo termine si può riscrivere di modo che
![$\aligned
T'_{\mu\rho\sigma}
&=\left\{
-\dfrac{2e^2\mu^{3(2-\omega)}}{(4\pi)^...
...nolimits [\gamma_5\gamma_\mu\gamma_\rho\gamma_\sigma\gamma_\alpha]
\endaligned$](img287.png) e regolarizzando dimenticando il termine in
e regolarizzando dimenticando il termine in
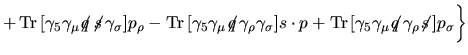 e gli
ordini superiori a e gli
ordini superiori a 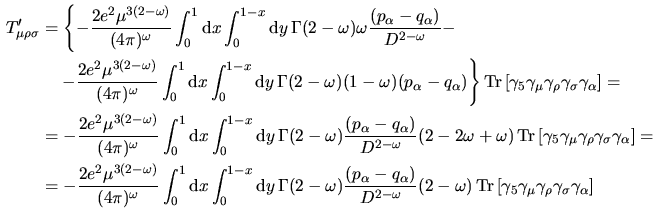 si ha che si ha che
![$\aligned
T'_{\mu\rho\sigma}&=
-\dfrac{e^2}{16\pi^2}\displaystyle\int _0^1{\rm...
...ot\hskip-0.18em{p}\,$}-\makebox{$\not\hskip-0.18em{q}\,$})]+\cdots
\endaligned$](img290.png) e calcolando la divergenza della corrente assiale e ricordando la I.42
e visto che, come detto sopra, i termini tralasciati si annullano si ha che
e calcolando la divergenza della corrente assiale e ricordando la I.42
e visto che, come detto sopra, i termini tralasciati si annullano si ha che
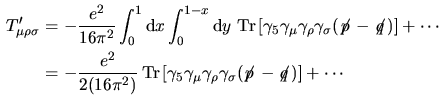 d' altra parte i termini simmetrici si annullano per cui
d' altra parte i termini simmetrici si annullano per cui
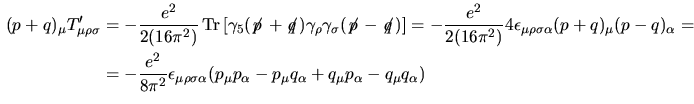 e dunque finalmente
e dunque finalmente
Allora si vede come calcolando con uno sviluppo perturbativo il termine  si ha che i diagrammi del primo tipo
danno i termini si ha che i diagrammi del primo tipo
danno i termini
![[*]](footnote.png) ma oltre a tale termine si aggiunge nello spazio degli impulsi un ulteriore
termine anomalo della forma I.82. Allora le usuali
Ward identities sono errate e in realtà esse sono della forma
ma oltre a tale termine si aggiunge nello spazio degli impulsi un ulteriore
termine anomalo della forma I.82. Allora le usuali
Ward identities sono errate e in realtà esse sono della forma
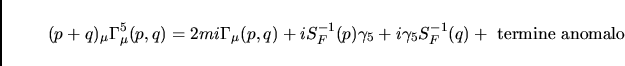 &=S_F(p)A_(p)T_(p,q)A_(q)S_F(-q)=
&=S_F(p)A_(p)T_(p,q)A_(q)S_F(-q)=
&&=-S_F(p)A_(p)T_(p,q)A_(q)S_F(q) e quindi le Ward identities anomale risultano &(p+q)__^5(p,q) &=2mi_(p,q)+i S^-1_F(p)_5+i_5S^-1_F(q)-iA_(p)A_(q)T_= &&=2mi_(p,q)+i S^-1_F(p)_5+i_5S^-1_F(q)-e^24^2_ p_q_A_(p)A_(q). && Ricordiamo che le I.58 si ricavano dall' espressione della divergenza di 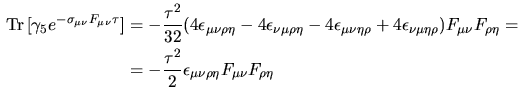 e del suo duale si ha che e del suo duale si ha che
 nello spazio degli impulsi come nello spazio degli impulsi come
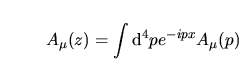 viene ora riscritto come
viene ora riscritto come
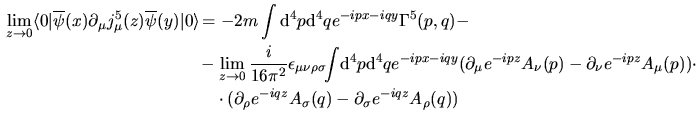 il termine aggiuntivo si ha che il termine aggiuntivo si ha che
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Comments
Comments
| Copyright© 1997-2006 Emiliano Bruni | Online from 16/08/1998 with |
Write me to:
|