 |


Next: L' anomalia ABJ con il
Up: Anomalie quantistiche
Previous: Le simmetrie interne
Un' altra simmetria di 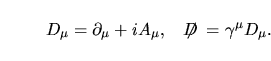 nel limite di massa nulla è la simmetria chiriale
globale
(x)&&'(x)=e^i_5(x) nel limite di massa nulla è la simmetria chiriale
globale
(x)&&'(x)=e^i_5(x)
(x)=^+(x)_0&&'(x)=(x) e^i_5
la cui semplice applicazione del solito teorema di Noether
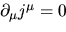 |
(4) |
porta a una corrente
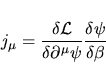 |
(5) |
la cui divergenza può essere calcolata utilizzando la variazione di 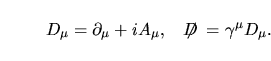 infatti
infatti
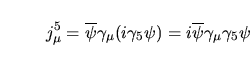 e integrando per parti e considerando la trasformazione chiriale come locale
ossia con
e integrando per parti e considerando la trasformazione chiriale come locale
ossia con
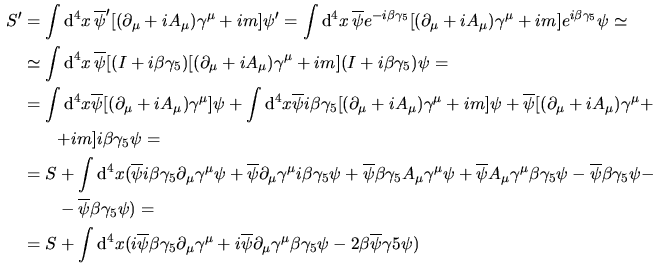 allora allora
![$\aligned
S'&=S+\displaystyle\int {\rm d}^4x\biggl\{i\beta\bigl[\overline{\psi}...
...\psi}\gamma_\mu\gamma_5\psi)-2m
\overline{\psi}\gamma_5\psi\bigr]
\endaligned$](img22.png) ma
ma 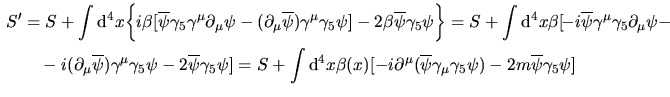 e dunque e dunque
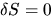 |
(6) |
o, nel limite di massa nulla
 |
(7) |
Ciò che voglianmo verificare ora è la conservazione di 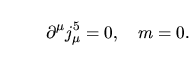 e di e di
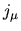 in presenza di correzzioni radioattive. Nessun problema ci viene da in presenza di correzzioni radioattive. Nessun problema ci viene da
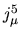 perche' dopo tutto esso è la corrente elettrica che noi sappiamo
essere conservata.
Per quanto riguarda invece la corrente chiriale è stato dimostrato da
Adler [1], Bell e Jackiw [2] che la sua conservazione
non è verificata ordini perche' dopo tutto esso è la corrente elettrica che noi sappiamo
essere conservata.
Per quanto riguarda invece la corrente chiriale è stato dimostrato da
Adler [1], Bell e Jackiw [2] che la sua conservazione
non è verificata ordini 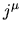 . A questa anomalia è la famosa
``ABJ chirial anomaly''.
I diagrammi contenenti vertici . A questa anomalia è la famosa
``ABJ chirial anomaly''.
I diagrammi contenenti vertici
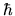 nell' elettrodinamica
degli spinori è di particolare interesse a causa delle sue molteplici
connessioni. Ciò che si vuole fare è mostrare che i diagrammi della
corrente chiriale hanno proprietà anomale che si differenziano da quelle
trovate dalla manipolazione formale dell' equazione dei campi. In particolare, a causa
della presenzadel diagramma a triangolo, la divergenza della corrente assiale
non sarà l' usuale espressione sopra calcolata e nell' elettrodinamica
degli spinori è di particolare interesse a causa delle sue molteplici
connessioni. Ciò che si vuole fare è mostrare che i diagrammi della
corrente chiriale hanno proprietà anomale che si differenziano da quelle
trovate dalla manipolazione formale dell' equazione dei campi. In particolare, a causa
della presenzadel diagramma a triangolo, la divergenza della corrente assiale
non sarà l' usuale espressione sopra calcolata e 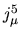 non soddisferà
più l' usuale Ward identity. Questo presenterà una connessione molto forte
con alcuni processi fisici quali i già citato tempo di decadimento non soddisferà
più l' usuale Ward identity. Questo presenterà una connessione molto forte
con alcuni processi fisici quali i già citato tempo di decadimento
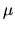 .
Utilizzando un procedimento introdotto da Fujikawa [3] basato sull' utilizzo
della funzione .
Utilizzando un procedimento introdotto da Fujikawa [3] basato sull' utilizzo
della funzione 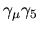 mostriamo che l' extra fattore anomalo proviene dal
fatto che l' elemento di misura funzionale non è invariante sotto trasformazioni
chiriali.
L' integrale di percorso mostriamo che l' extra fattore anomalo proviene dal
fatto che l' elemento di misura funzionale non è invariante sotto trasformazioni
chiriali.
L' integrale di percorso
![\begin{displaymath}
e^{-\Cal Z[A]}=\int\Cal D\psi\Cal D\psi^+ e^{-S[\psi,\psi^+,A_\mu]}
\end{displaymath}](img32.png) |
(8) |
dove 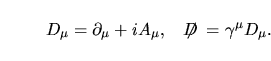 è definita nella I.1, può essere formalmente integrata come è definita nella I.1, può essere formalmente integrata come
![\begin{displaymath}
e^{-\Cal Z[A]}=\det\bigl[\gamma_\mu(\partial_\mu+iA_\mu)+im\bigr]l.
\end{displaymath}](img33.png) |
(9) |
Cosa accade ora a tale integrale di percorso quando si
opera una trasformazione chiriale. Già sappiamo che 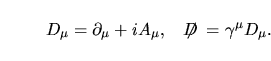 è invariante se è invariante se 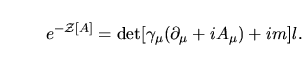 è una variabile globale e
è una variabile globale e 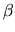 ma cosa succede all' elemento di
misura ma cosa succede all' elemento di
misura
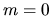 ? È ovvio che esso varierà come ? È ovvio che esso varierà come
dove ![$J[\beta]$](img38.png) è lo jacobiano della trasformazione chiriale. Ciò che si
deve fare allora è calcolare questo jacobiano.
D' altra parte, è lo jacobiano della trasformazione chiriale. Ciò che si
deve fare allora è calcolare questo jacobiano.
D' altra parte,  e e 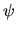 sono variabili d' integrazione per
cui l' F.P.I. deve rimanere inalterato formalmente se a sono variabili d' integrazione per
cui l' F.P.I. deve rimanere inalterato formalmente se a  e a e a 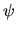 si sostituisce
si sostituisce 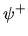 e e 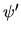 ossia, in particolare, se ossia, in particolare, se  e
e 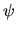 variano per una trasformazione chiriale infinitesiama variano per una trasformazione chiriale infinitesiama
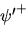 |
(10) |
deve essere che
![\begin{displaymath}
\int{\Cal D}\psi{\Cal D}\psi^+ m^{-S[\psi,\psi^+,A_\mu]}=\...
...}=
\int\Cal D\psi'\Cal D{\psi'}^+ e^{-S'[\psi,\psi^+,A_\mu]}
\end{displaymath}](img44.png) |
(11) |
dove 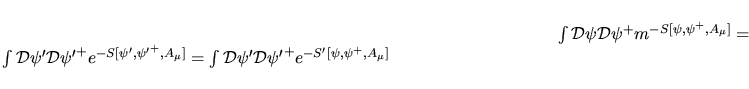 denota l' azione trasformata dalla trasformazione chiriale, che
già sappiamo essere denota l' azione trasformata dalla trasformazione chiriale, che
già sappiamo essere
![\begin{displaymath}
S'=S+\displaystyle\int {\rm d}^4x\beta(x)\bigl[-i\partial_\...
...gamma_\mu\gamma_5\psi)-
2m\overline{\psi}\gamma_5\psi\bigr].
\end{displaymath}](img46.png) |
(12) |
Ma allora l' integrale di cammino a destra della I.13 può essere
formalmente integrata nell' euclideo come
![$\aligned
\displaystyle\int \Cal D\psi'\Cal D{\psi'}^+ e^{-S[\psi,\psi^+,A_\mu]...
...iA_\mu)+im-i\beta\partial_\mu\gamma_\mu
\gamma_5-2m\beta\gamma_5)
\endaligned$](img47.png) da cui
da cui
![\begin{displaymath}
\det\bigl[\gamma_\mu(\partial_\mu+iA_\mu)+im\bigr]=J[\beta...
...i\beta\partial_\mu\gamma_\mu\gamma_5
-2m\beta\gamma_5\bigr].
\end{displaymath}](img48.png) |
(13) |
Per prudenza moltiplichiamo ora tale espressione con l' analoga in cui si è
scambiata
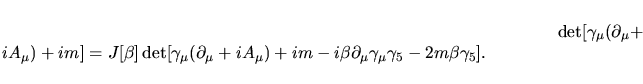 in modo da dover trattare con determinanti di operatori
ellittici con i quali la tecnica della funzione in modo da dover trattare con determinanti di operatori
ellittici con i quali la tecnica della funzione  riesce meglio, ossia utilizziamo
la riesce meglio, ossia utilizziamo
la
![$\aligned
\det\bigl[(\makebox{$\not\hskip-0.35em{D}\,$}+im)(\makebox{$\not\hski...
...eta\partial_\mu\gamma_\mu\gamma_5+\\
&\quad+2m\beta\gamma_5)\bigr]\endaligned$](img50.png)
![$\aligned\det[\makebox{$\not\hskip-0.35em{D}\,$}^2+m^2]&=J^2[\beta]\det[\makebox...
...-0.35em{D}\,$},\beta\}\gamma_5+4m^2i\beta\gamma_5+o(\beta^2)\bigr]
\endaligned$](img51.png) e detto con
e detto con
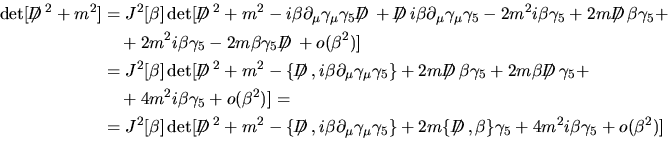 |
(14) |
si ha che una soluzione formale per ![$J^2[\beta]$](img53.png) risulta risulta
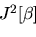 |
(15) |
o anche, passando ai logaritmi
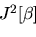 |
(16) |
che, ordine 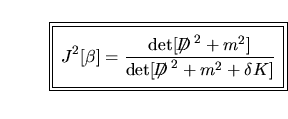 può essere scritto come può essere scritto come
![\begin{displaymath}
\ln J[\beta]=-\dfrac12\displaystyle\int {\rm d}^4x\,\beta(x...
...p-0.35em{D}\,$}^2+m^2+\delta K]\right\}\right\vert _{\beta=0}
\end{displaymath}](img56.png) |
(17) |
o anche, ricordando che
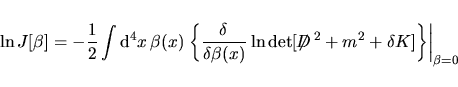 |
(18) |
si ha che
![\begin{displaymath}
\ln J[\beta]=\frac12\displaystyle\int {\rm d}^4x\,\beta(x)...
...4em{D}\,$}^2+m^2+\delta K]}(0)\right\}\right\vert _{\beta=0}.
\end{displaymath}](img58.png) |
(19) |
Ricordiamo ora alcune cose sulla funzione 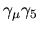 ; per un ben definito operatore ; per un ben definito operatore 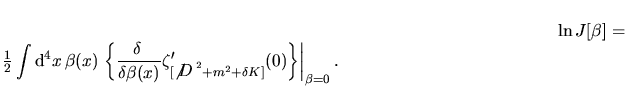 agente su
agente su 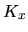 la la 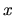 risulta data da risulta data da
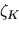 |
(20) |
dove la traccia agisce su tutti gli indici di 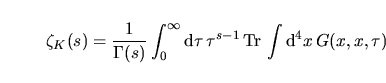 e e 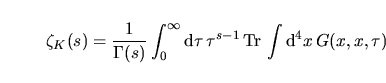 soddisfa la così
detta equazione del calore soddisfa la così
detta equazione del calore
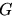 |
(21) |
Allora la variazione della 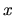 dovuta ad una variazione dell' operatore dovuta ad una variazione dell' operatore 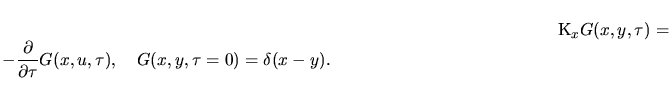 può essere scritta come
può essere scritta come
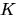 |
(22) |
dove ora la
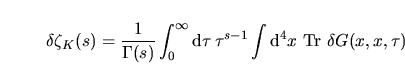 soddisfa l' equazione del calore inomogenea
ottenuta differenziando l' omogenea come soddisfa l' equazione del calore inomogenea
ottenuta differenziando l' omogenea come
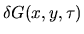 ossia la ossia la
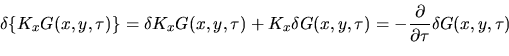 |
(23) |
Per sostituzione si può vedere che una soluzione per la I.25
risulta
 |
(24) |
infatti differenziando rispetto a 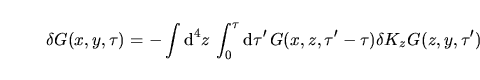
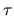 da cui la I.25.
D' altra parte esiste un modo per costruire la
da cui la I.25.
D' altra parte esiste un modo per costruire la 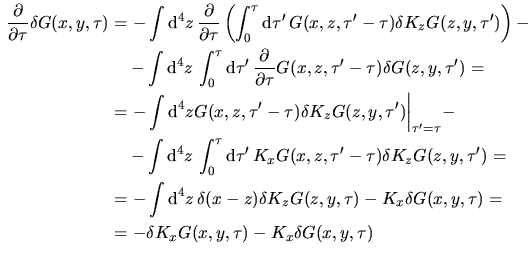 dagli autovalori
dell' operatore dagli autovalori
dell' operatore 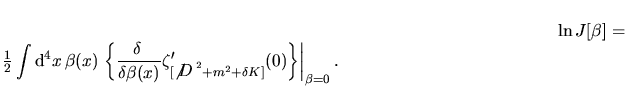 [4] infatti detta con [4] infatti detta con 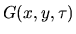 una base delle
soluzionui di una base delle
soluzionui di 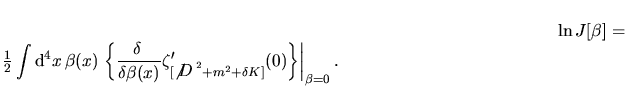 con con 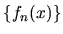 come autovalore ossia tale che
K_xf_n(x)&=&_n f_n(x) come autovalore ossia tale che
K_xf_n(x)&=&_n f_n(x)
d^4x f^+_n(x)f_n(x)&=&_nm
si ha che la
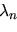 |
(25) |
soddisfa proprio la I.23 ma allora
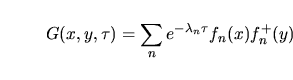 e integrando in
e integrando in 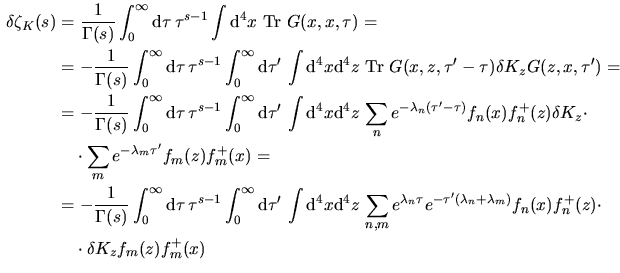
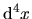 e detto con
e detto con
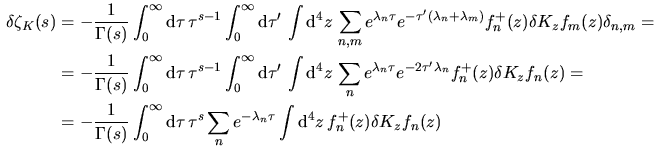
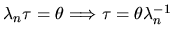 e dunque, infine,
e dunque, infine,
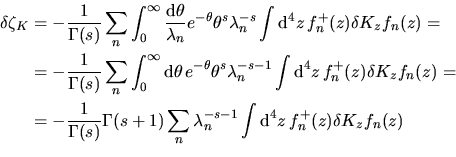 |
(26) |
Applichiamo ora questo formalismo al nostro problema. Posto
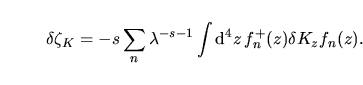 con con
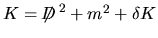 si ha che si ha che
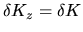 e dunque e dunque
![$\aligned
\left.\dfrac{\delta\zeta_K(s)}{\delta\beta(x)}\right\vert _{\beta=0}
...
...gl.\bigl.+o(\beta^2)\bigr]
f_n(z)\Biggr\}
\right\vert _{\beta=0}
\endaligned$](img86.png) d' altra parte gli ordini superiori a
d' altra parte gli ordini superiori a 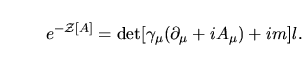 nella derivazione danno termini
contenenti nella derivazione danno termini
contenenti 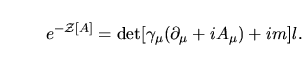 che dunque si annullano per che dunque si annullano per 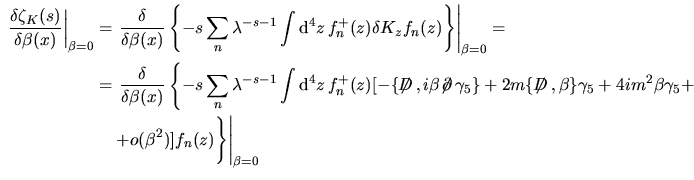 per cui possiamo
tralasciare gli per cui possiamo
tralasciare gli  per cui per cui
![$\aligned
\left.\dfrac{\delta\zeta_K(s)}{\delta\beta(x)}\right\vert _{\beta=0}
...
...+
4im^2\beta\gamma_5\bigr]
f_n(z)\Biggr\}
\right\vert _{\beta=0}.\endaligned$](img89.png) Ora, ovviamente anche
Ora, ovviamente anche
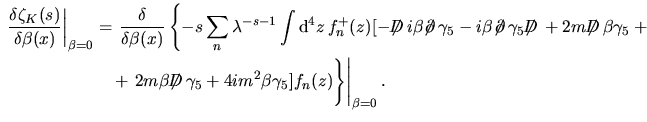 è diagonalizzabile sulla stessa base
di è diagonalizzabile sulla stessa base
di
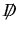 e siano e siano 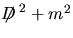 gli autovalori antihermitiano di gli autovalori antihermitiano di
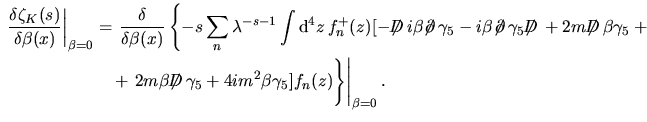 tale che
tale che
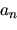 |
(27) |
dove l' ultima delle I.31 proviene dal fatto che
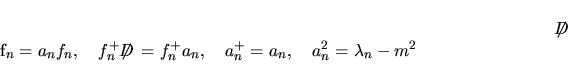 |
(28) |
Allora si ha che
![$\aligned
\left.\dfrac{\delta\zeta_K(s)}{\delta\beta(x)}\right\vert _{\beta=0}
...
...\!
4im^2\beta\gamma_5\bigr]
f_n(z)\right\}
\right\vert _{\beta=0}\endaligned$](img95.png) Ciò che facciamo ora è quello di aggiungere e togliere il termine
Ciò che facciamo ora è quello di aggiungere e togliere il termine
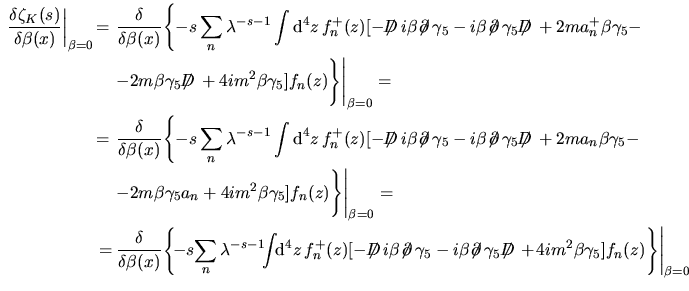 di modo che di modo che
![$\aligned
\left.\dfrac{\delta\zeta_K(s)}{\delta\beta(x)}\right\vert _{\beta=0}
...
...ot\hskip-0.35em{D}\,$}\bigr]
f_n(z)\Biggr\}
\right\vert _{\beta=0}\endaligned$](img97.png) e d' altra parte
e d' altra parte
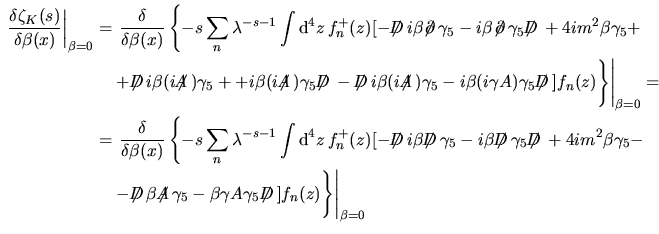 è esso stesso diagonalizzabile su è esso stesso diagonalizzabile su 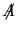 ma essendo
un operatore antiherimitiano allora ma essendo
un operatore antiherimitiano allora
![[*]](file:/usr/share/latex2html/icons/footnote.png)
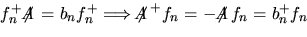 |
(29) |
e dunque facendolo agire sugli autostati
 e dunque si elidono a vicenda. Allora si ha che
e dunque si elidono a vicenda. Allora si ha che
![$\aligned
\left.\dfrac{\delta\zeta_K(s)}{\delta\beta(x)}\right\vert _{\beta=0}
...
...d+4im^2\beta\gamma_5
\bigr]
f_n(z)\Biggr\}
\right\vert _{\beta=0}\endaligned$](img103.png)
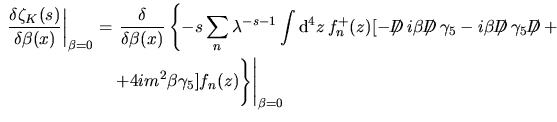 e ricorando che
e ricorando che
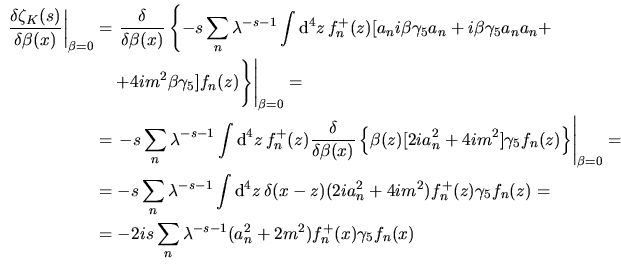 allora allora
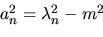 |
(30) |
e inserendo questo risultato nella I.21 si è trovato che
![\begin{displaymath}
\ln J[\beta]=-\left.-i\int{\rm d}^4x\,\beta(x)\left\{\dfra...
...mbda_n+m^2)f_n^+(x)\gamma_5 f_n(x)\right\}\right\vert _{s=0}.
\end{displaymath}](img107.png) |
(31) |
Ciò che rimane da fare ora è calcolare la sommatoria. Ma prima di farlo
analizziamo l' espressione
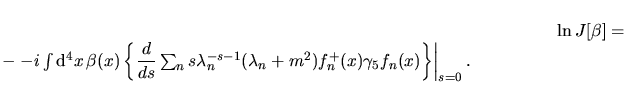 . Esso può essere pensato come una sorta
di conteggio del numero di autovettori con autovalore nullo ( i cosi detti
``zero modes''). Infatti . Esso può essere pensato come una sorta
di conteggio del numero di autovettori con autovalore nullo ( i cosi detti
``zero modes''). Infatti
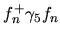 esistono due autovettori esistono due autovettori
 e e
 e nella sommatoria della I.35 per ogni e nella sommatoria della I.35 per ogni 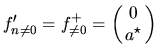 c' e sia un termine della forma
c' e sia un termine della forma
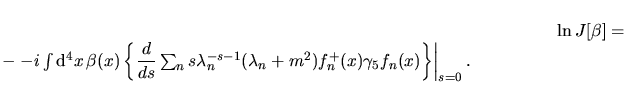 e sia un termine e sia un termine
 per cui per ogni
per cui per ogni 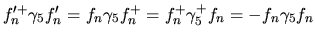 i termini si elidono a vicenda.
Gli unici termini non nulli sono proprio quelli corrispondenti all' autovalore
nullo per cui tale somma sarà certamente proporzionale a i termini si elidono a vicenda.
Gli unici termini non nulli sono proprio quelli corrispondenti all' autovalore
nullo per cui tale somma sarà certamente proporzionale a
![[*]](file:/usr/share/latex2html/icons/footnote.png)
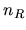 ossia
al numero netto di zero modes.
Calcoliamo dunque la somma ossia
al numero netto di zero modes.
Calcoliamo dunque la somma
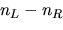 |
(32) |
questa può essere riscritta in forma operatoriale come
![$\aligned C(s)&=s\sum_n(\lambda_n^{-s}+\lambda_n{-s-1}m^2)f_n^+(x)\gamma_5f_n(x)...
...amma_5(\makebox{$\not\hskip-0.35em{D}\,$}^2+m^2)^{-s-1}f_n(x)\bigr].\endaligned$](img119.png) Ora, la sommatoria non è ben definita a causa della
Ora, la sommatoria non è ben definita a causa della 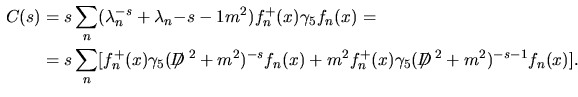 introdotta dal prodotto introdotta dal prodotto
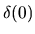 e dunque, per eliminare formalmente tale infinito poniamo e dunque, per eliminare formalmente tale infinito poniamo
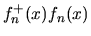 ossia ossia
![$\aligned
C(s)
&=\lim\limits_{x\to y}s\sum_n\bigl[f_n^+(y)\gamma_5(\makebox{$\...
...x{$\not\hskip-0.35em{D}\,$}^2+m^2)^{-s-1}\bigr]\delta(x-y)\Bigr\}.
\endaligned$](img123.png) Utilizzando ora la rappresentazione integrale per l' operatore
Utilizzando ora la rappresentazione integrale per l' operatore
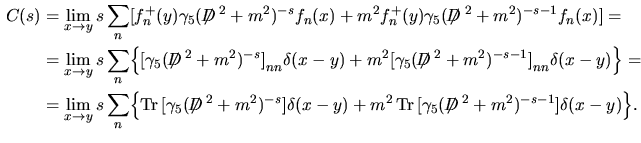 e per la
e per la 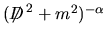 ossia la ossia la
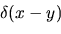 |
(33) |
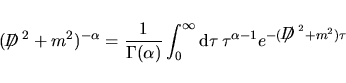 |
(34) |
otteniamo
![$C(s)=\lim\limits_{x\to y}\!\dfrac1{\Gamma(s)}\displaystyle\int \!\dfrac{{\rm d}...
..._5e^{-(\makebox{$\not\hskip-0.35em{D}\,$}^2+m^2)\tau}
\bigr]\right\}e^{i(x-y)}$](img128.png) essendo
essendo
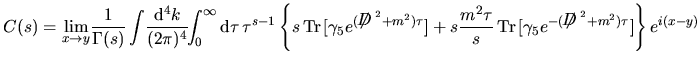 .
L' utilità di tutto questo costrutto sta nel fatto che ora l' operatore .
L' utilità di tutto questo costrutto sta nel fatto che ora l' operatore
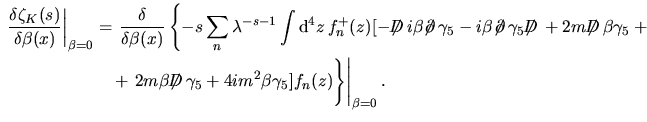 diventa più maneggiabile visto che ora, agendo sull' esponenziale, il
diventa più maneggiabile visto che ora, agendo sull' esponenziale, il 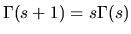 tira fuori un tira fuori un 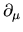 . Scriviamo ora . Scriviamo ora
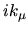 d' altra parte il commutatore e antisimmetrico mentre
d' altra parte il commutatore e antisimmetrico mentre
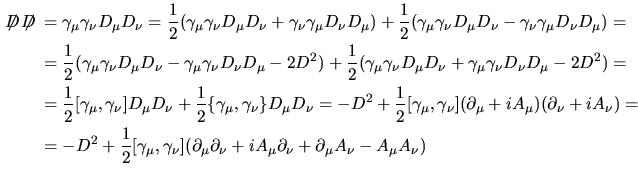 e
e 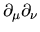 sono termini simmetrici e dunque non danno contributi
e se anche sono termini simmetrici e dunque non danno contributi
e se anche
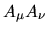 si annulla si annulla
![[*]](file:/usr/share/latex2html/icons/footnote.png) si ha che
si ha che

\endaligned$](img136.png) e detto con
e detto con
![\begin{displaymath}
\sigma_{\mu\nu}=\frac i4[\gamma_\mu,\gamma_\nu]
\end{displaymath}](img137.png) |
(35) |
ed essendo
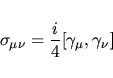 |
(36) |
si ha che
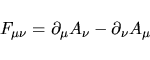 |
(37) |
per cui
![$\mathop{\famzero Tr\,}\nolimits [\gamma_5e^{-(\makebox{$\not\hskip-0.35em{D}\,$...
...u}\mathop{\famzero Tr\,}\nolimits [\gamma_5e^{-\sigma_{\mu\nu}F_{\mu\nu}\tau)}]$](img140.png) e, sviluppando l' esponenziale dentro alla traccia in serie di Taylor
e, sviluppando l' esponenziale dentro alla traccia in serie di Taylor
![$\aligned
\mathop{\famzero Tr\,}\nolimits [\gamma_5e^{-\sigma_{\mu\nu} F_{\mu\n...
...\sigma_{\mu\nu} F_{\mu\nu}\sigma_{\rho\eta}F_{\rho\eta}]+o(\tau^2)
\endaligned$](img141.png) ma
ma
![$\mathop{\famzero Tr\,}\nolimits [\gamma_5]=0$](img142.png) , ,
![$\mathop{\famzero Tr\,}\nolimits [\gamma_5\sigma_{\mu\nu}]\propto\mathop{\famzer...
...
\gamma_nu]-\mathop{\famzero Tr\,}\nolimits [\gamma_5\gamma_\nu\gamma_\mu=0-0=0$](img143.png) e se anche gli
e se anche gli 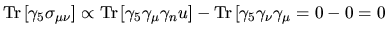 sono nulli sono nulli
![[*]](file:/usr/share/latex2html/icons/footnote.png) si ha che
si ha che
![$\aligned
\mathop{\famzero Tr\,}\nolimits [\gamma_5e^{-\sigma_{\mu\nu} F_{\mu\n...
..._\nu\gamma_\mu\gamma_\eta\gamma_\rho]\bigr\}F_{\mu\nu}F_{\rho
\eta}\endaligned$](img145.png) ed essendo
ed essendo
![\begin{displaymath}
\mathop{\famzero Tr\,}\nolimits [
\gamma_5\gamma_\mu\gamma_\nu\gamma_\rho\gamma_\eta]=4\epsilon_{\mu\nu\rho\eta}
\end{displaymath}](img146.png) |
(38) |
allora
 e definito il tensore duale di
e definito il tensore duale di 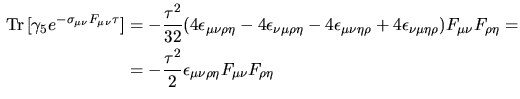 come come
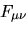 |
(39) |
si ha che
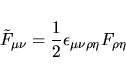 |
(40) |
e sostituito nella 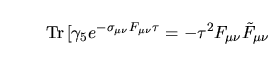 tale risultato si ha che tale risultato si ha che
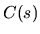 d' altra parte
d' altra parte
![$\aligned e^{D^2\tau}e^{ik(x-y)}&=
\dsize\sum _{n=0}^\infty\dfrac1{n!}\bigl[(\p...
...au\bigr]^ne^{ik(x-y)}=\\
&=
e^{-(k^2+2k_\mu A_mu+A^2)}e^{ik(x-y)}\endaligned$](img153.png) e d'altra parte è ora possibile eseguire il limite in quanto con la derivazione
si è persa la presenza della
e d'altra parte è ora possibile eseguire il limite in quanto con la derivazione
si è persa la presenza della 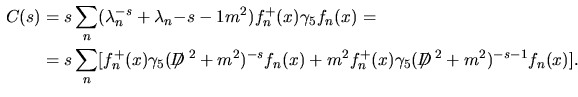
![[*]](file:/usr/share/latex2html/icons/footnote.png) e, posto
e, posto
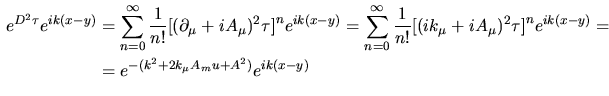 allora allora
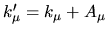 e posto
e posto
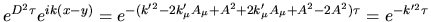 si ha che si ha che
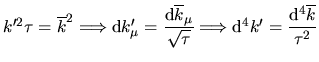 e d' altra parte e d' altra parte
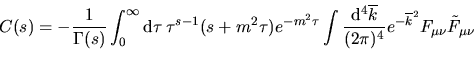 |
(41) |
per cui
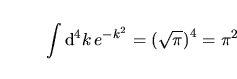 ma ma
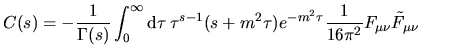 per cui
per cui
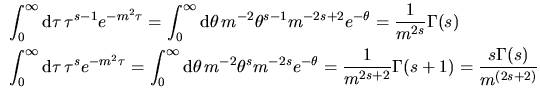 e quindi in definitiva e quindi in definitiva
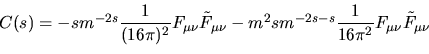 |
(42) |
e sostituendo nella I.35
![$\ln J[\beta]=-i\displaystyle\int {\rm d}^4x\,\beta(x)\left.\left\{
\dfrac{d{}}...
... d}^4x\,\beta(x)\left\{
\dfrac{1}{8\pi^2}F_{\mu\nu}\tilde F_{\mu\nu}
\right\}$](img163.png) e quindi si è trovato che
e quindi si è trovato che
![\begin{displaymath}
\ln J[\beta]=\dfrac{i}{8\pi^2}\displaystyle\int {\rm d}^4x\,\beta(x) F_{\mu\nu}
\tilde F_{\mu\nu}
\end{displaymath}](img164.png) |
(43) |
e ricordando la I.13 si ha che
![$-S=-S'+\ln[\beta]=-S-\displaystyle\int {\rm d}^4x\,\beta(x)\bigl[-i\partial_\mu...
...si}\gamma_\mu\gamma_5\psi)-2m\overline{\psi}\gamma_5\psi\bigr]+\ln[\beta]\qquad$](img165.png) da cui da cui
![$\displaystyle\int \beta(X)\left[i\partial_\mu(\overline{\psi}\gamma_\mu\gamma_5...
...}
\gamma_5\psi+\dfrac i{8\pi^2}F_{\mu\nu}\tilde F_{\mu\nu}\right]{\rm d}^4 x=0$](img166.png) e quindi si ottiene la legge di conservazione anomala per la corrente chiriale
e quindi si ottiene la legge di conservazione anomala per la corrente chiriale
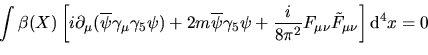 |
(44) |
e dunque
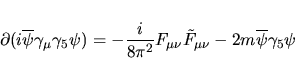 |
(45) |
per cui si vede come anche nel limite di massa nulla la corrente che nell' azione
veniva conservata acquista nell' integrazione funzionale un termine anomalo detto
di Adler-Bell-Jackwin della forma
 |
(46) |


Next: L' anomalia ABJ con il
Up: Anomalie quantistiche
Previous: Le simmetrie interne
|
 |
|
 |


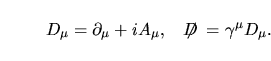 nel limite di massa nulla è la simmetria chiriale
globale
(x)&&'(x)=e^i_5(x)
nel limite di massa nulla è la simmetria chiriale
globale
(x)&&'(x)=e^i_5(x)
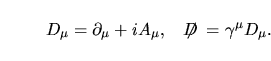 infatti
infatti
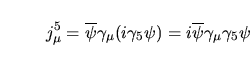 e integrando per parti e considerando la trasformazione chiriale come locale
ossia con
e integrando per parti e considerando la trasformazione chiriale come locale
ossia con 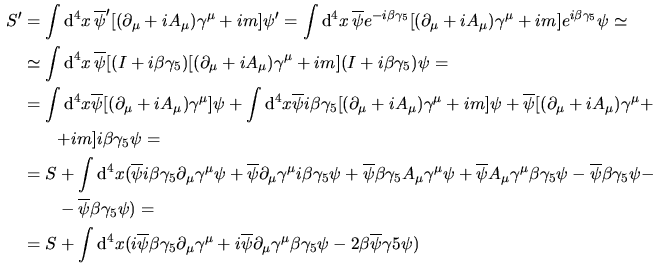 allora
allora
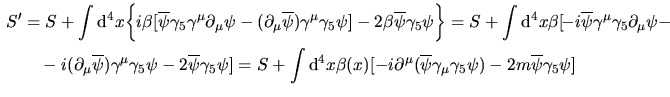 e dunque
e dunque
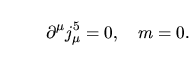 e di
e di
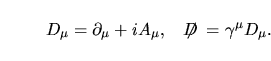 è definita nella I.1, può essere formalmente integrata come
è definita nella I.1, può essere formalmente integrata come
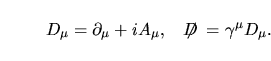 è invariante se
è invariante se 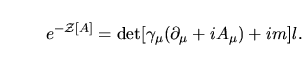 è una variabile globale e
è una variabile globale e ![$J[\beta]$](img38.png) è lo jacobiano della trasformazione chiriale. Ciò che si
deve fare allora è calcolare questo jacobiano.
D' altra parte,
è lo jacobiano della trasformazione chiriale. Ciò che si
deve fare allora è calcolare questo jacobiano.
D' altra parte, 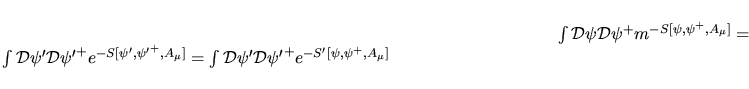 denota l' azione trasformata dalla trasformazione chiriale, che
già sappiamo essere
denota l' azione trasformata dalla trasformazione chiriale, che
già sappiamo essere
![$\aligned
\displaystyle\int \Cal D\psi'\Cal D{\psi'}^+ e^{-S[\psi,\psi^+,A_\mu]...
...iA_\mu)+im-i\beta\partial_\mu\gamma_\mu
\gamma_5-2m\beta\gamma_5)
\endaligned$](img47.png) da cui
da cui
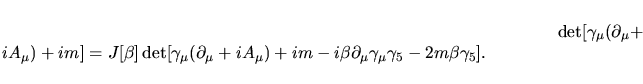 in modo da dover trattare con determinanti di operatori
ellittici con i quali la tecnica della funzione
in modo da dover trattare con determinanti di operatori
ellittici con i quali la tecnica della funzione ![$\aligned\det[\makebox{$\not\hskip-0.35em{D}\,$}^2+m^2]&=J^2[\beta]\det[\makebox...
...-0.35em{D}\,$},\beta\}\gamma_5+4m^2i\beta\gamma_5+o(\beta^2)\bigr]
\endaligned$](img51.png) e detto con
e detto con
![$J^2[\beta]$](img53.png) risulta
risulta
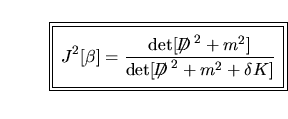 può essere scritto come
può essere scritto come
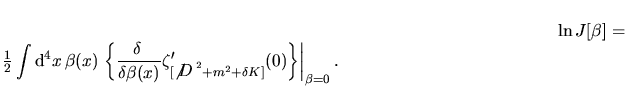 agente su
agente su 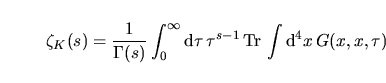 e
e 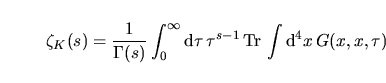 soddisfa la così
detta equazione del calore
soddisfa la così
detta equazione del calore
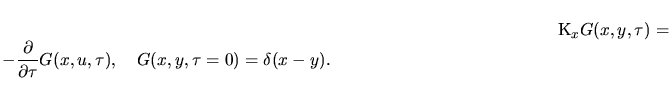 può essere scritta come
può essere scritta come
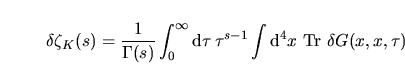 soddisfa l' equazione del calore inomogenea
ottenuta differenziando l' omogenea come
soddisfa l' equazione del calore inomogenea
ottenuta differenziando l' omogenea come
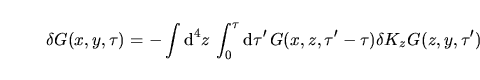
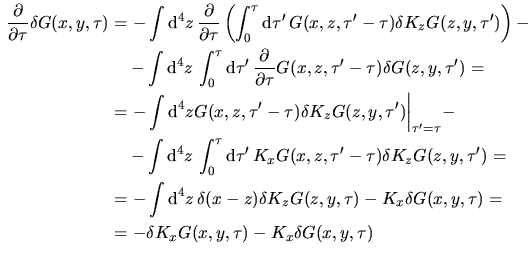 dagli autovalori
dell' operatore
dagli autovalori
dell' operatore 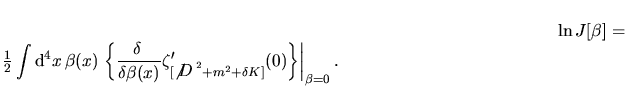 [4] infatti detta con
[4] infatti detta con 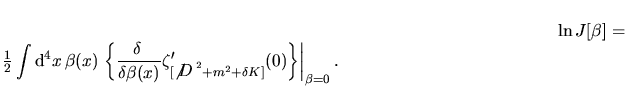 con
con 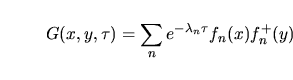 e integrando in
e integrando in 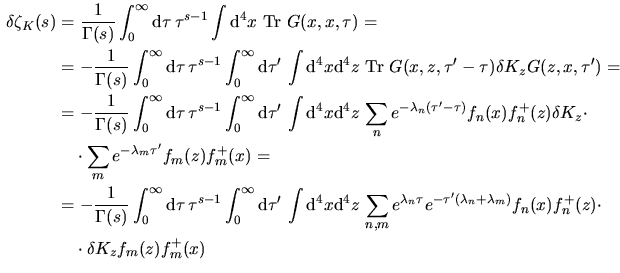
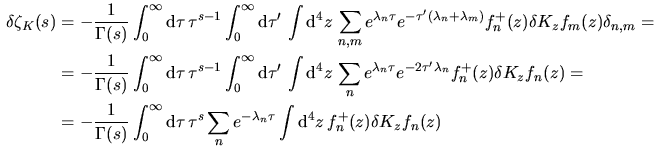
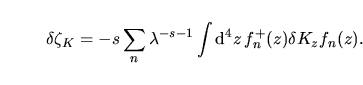 con
con
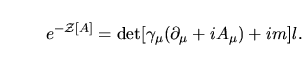 nella derivazione danno termini
contenenti
nella derivazione danno termini
contenenti 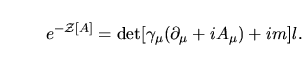 che dunque si annullano per
che dunque si annullano per 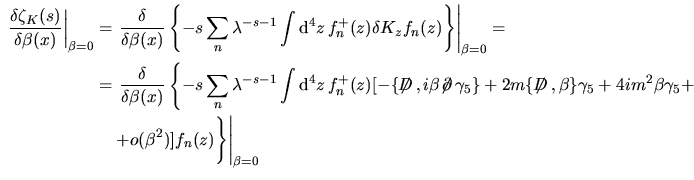 per cui possiamo
tralasciare gli
per cui possiamo
tralasciare gli 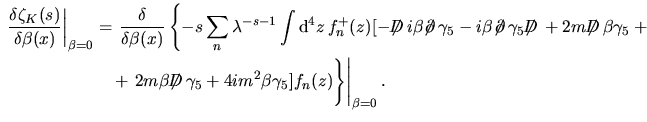 è diagonalizzabile sulla stessa base
di
è diagonalizzabile sulla stessa base
di
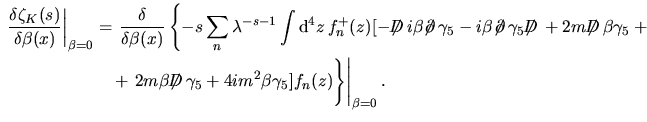 tale che
tale che
![$\aligned
\left.\dfrac{\delta\zeta_K(s)}{\delta\beta(x)}\right\vert _{\beta=0}
...
...\!
4im^2\beta\gamma_5\bigr]
f_n(z)\right\}
\right\vert _{\beta=0}\endaligned$](img95.png) Ciò che facciamo ora è quello di aggiungere e togliere il termine
Ciò che facciamo ora è quello di aggiungere e togliere il termine
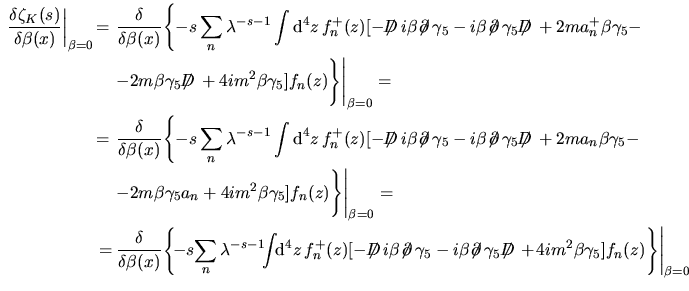 di modo che
di modo che
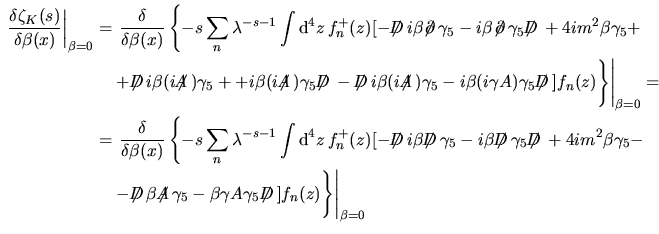 è esso stesso diagonalizzabile su
è esso stesso diagonalizzabile su  e dunque si elidono a vicenda. Allora si ha che
e dunque si elidono a vicenda. Allora si ha che
![$\aligned
\left.\dfrac{\delta\zeta_K(s)}{\delta\beta(x)}\right\vert _{\beta=0}
...
...d+4im^2\beta\gamma_5
\bigr]
f_n(z)\Biggr\}
\right\vert _{\beta=0}\endaligned$](img103.png)
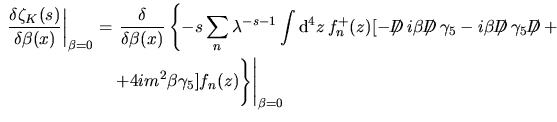 e ricorando che
e ricorando che
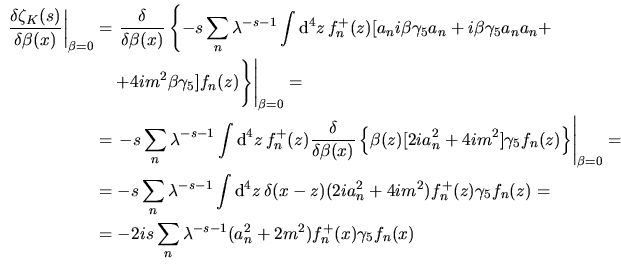 allora
allora
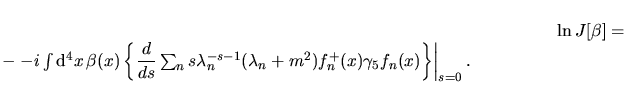 . Esso può essere pensato come una sorta
di conteggio del numero di autovettori con autovalore nullo ( i cosi detti
``zero modes''). Infatti
. Esso può essere pensato come una sorta
di conteggio del numero di autovettori con autovalore nullo ( i cosi detti
``zero modes''). Infatti
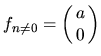 e nella sommatoria della I.35 per ogni
e nella sommatoria della I.35 per ogni 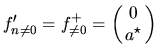 c' e sia un termine della forma
c' e sia un termine della forma
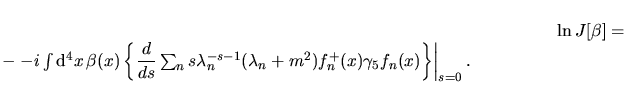 e sia un termine
e sia un termine
![$\aligned C(s)&=s\sum_n(\lambda_n^{-s}+\lambda_n{-s-1}m^2)f_n^+(x)\gamma_5f_n(x)...
...amma_5(\makebox{$\not\hskip-0.35em{D}\,$}^2+m^2)^{-s-1}f_n(x)\bigr].\endaligned$](img119.png) Ora, la sommatoria non è ben definita a causa della
Ora, la sommatoria non è ben definita a causa della 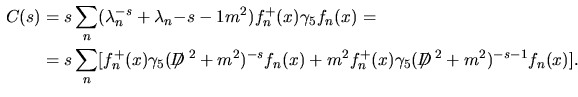 introdotta dal prodotto
introdotta dal prodotto
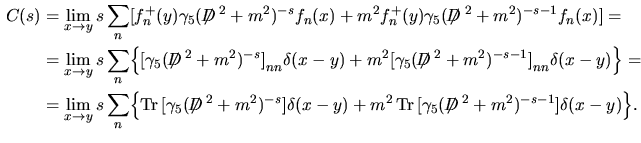 e per la
e per la ![$C(s)=\lim\limits_{x\to y}\!\dfrac1{\Gamma(s)}\displaystyle\int \!\dfrac{{\rm d}...
..._5e^{-(\makebox{$\not\hskip-0.35em{D}\,$}^2+m^2)\tau}
\bigr]\right\}e^{i(x-y)}$](img128.png) essendo
essendo
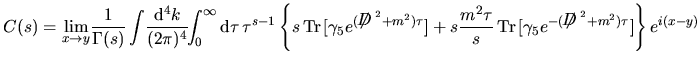 .
L' utilità di tutto questo costrutto sta nel fatto che ora l' operatore
.
L' utilità di tutto questo costrutto sta nel fatto che ora l' operatore
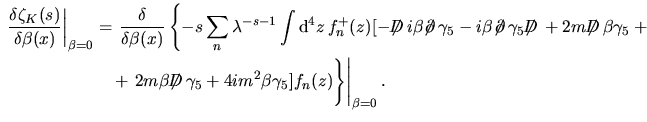 diventa più maneggiabile visto che ora, agendo sull' esponenziale, il
diventa più maneggiabile visto che ora, agendo sull' esponenziale, il 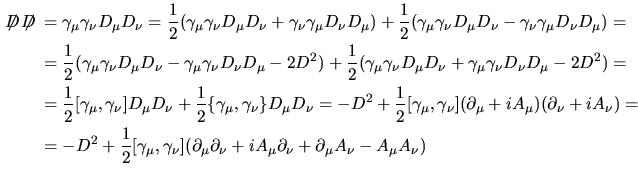 e
e ![$\mathop{\famzero Tr\,}\nolimits [\gamma_5e^{-(\makebox{$\not\hskip-0.35em{D}\,$...
...u}\mathop{\famzero Tr\,}\nolimits [\gamma_5e^{-\sigma_{\mu\nu}F_{\mu\nu}\tau)}]$](img140.png) e, sviluppando l' esponenziale dentro alla traccia in serie di Taylor
e, sviluppando l' esponenziale dentro alla traccia in serie di Taylor
![$\aligned
\mathop{\famzero Tr\,}\nolimits [\gamma_5e^{-\sigma_{\mu\nu} F_{\mu\n...
...\sigma_{\mu\nu} F_{\mu\nu}\sigma_{\rho\eta}F_{\rho\eta}]+o(\tau^2)
\endaligned$](img141.png) ma
ma
![$\mathop{\famzero Tr\,}\nolimits [\gamma_5]=0$](img142.png) ,
,
 e definito il tensore duale di
e definito il tensore duale di 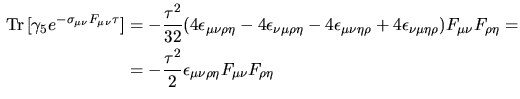 come
come
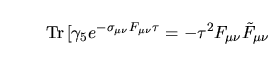 tale risultato si ha che
tale risultato si ha che
![$\aligned e^{D^2\tau}e^{ik(x-y)}&=
\dsize\sum _{n=0}^\infty\dfrac1{n!}\bigl[(\p...
...au\bigr]^ne^{ik(x-y)}=\\
&=
e^{-(k^2+2k_\mu A_mu+A^2)}e^{ik(x-y)}\endaligned$](img153.png) e d'altra parte è ora possibile eseguire il limite in quanto con la derivazione
si è persa la presenza della
e d'altra parte è ora possibile eseguire il limite in quanto con la derivazione
si è persa la presenza della 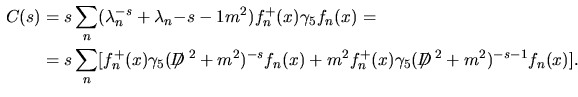
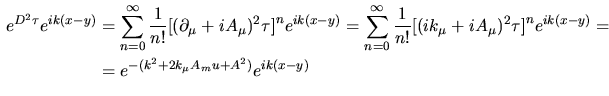 allora
allora
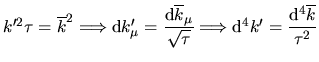 e d' altra parte
e d' altra parte
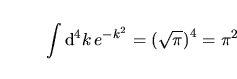 ma
ma
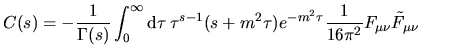 per cui
per cui
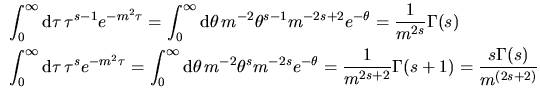 e quindi in definitiva
e quindi in definitiva
![$\ln J[\beta]=-i\displaystyle\int {\rm d}^4x\,\beta(x)\left.\left\{
\dfrac{d{}}...
... d}^4x\,\beta(x)\left\{
\dfrac{1}{8\pi^2}F_{\mu\nu}\tilde F_{\mu\nu}
\right\}$](img163.png) e quindi si è trovato che
e quindi si è trovato che
![$-S=-S'+\ln[\beta]=-S-\displaystyle\int {\rm d}^4x\,\beta(x)\bigl[-i\partial_\mu...
...si}\gamma_\mu\gamma_5\psi)-2m\overline{\psi}\gamma_5\psi\bigr]+\ln[\beta]\qquad$](img165.png) da cui
da cui
![$\displaystyle\int \beta(X)\left[i\partial_\mu(\overline{\psi}\gamma_\mu\gamma_5...
...}
\gamma_5\psi+\dfrac i{8\pi^2}F_{\mu\nu}\tilde F_{\mu\nu}\right]{\rm d}^4 x=0$](img166.png) e quindi si ottiene la legge di conservazione anomala per la corrente chiriale
e quindi si ottiene la legge di conservazione anomala per la corrente chiriale
 Commenti
Commenti